Minitab adalah salah satu softwaree yang dirancang untuk mengolah data statistika dengan lebih mudah daripada menghitung secara manual.
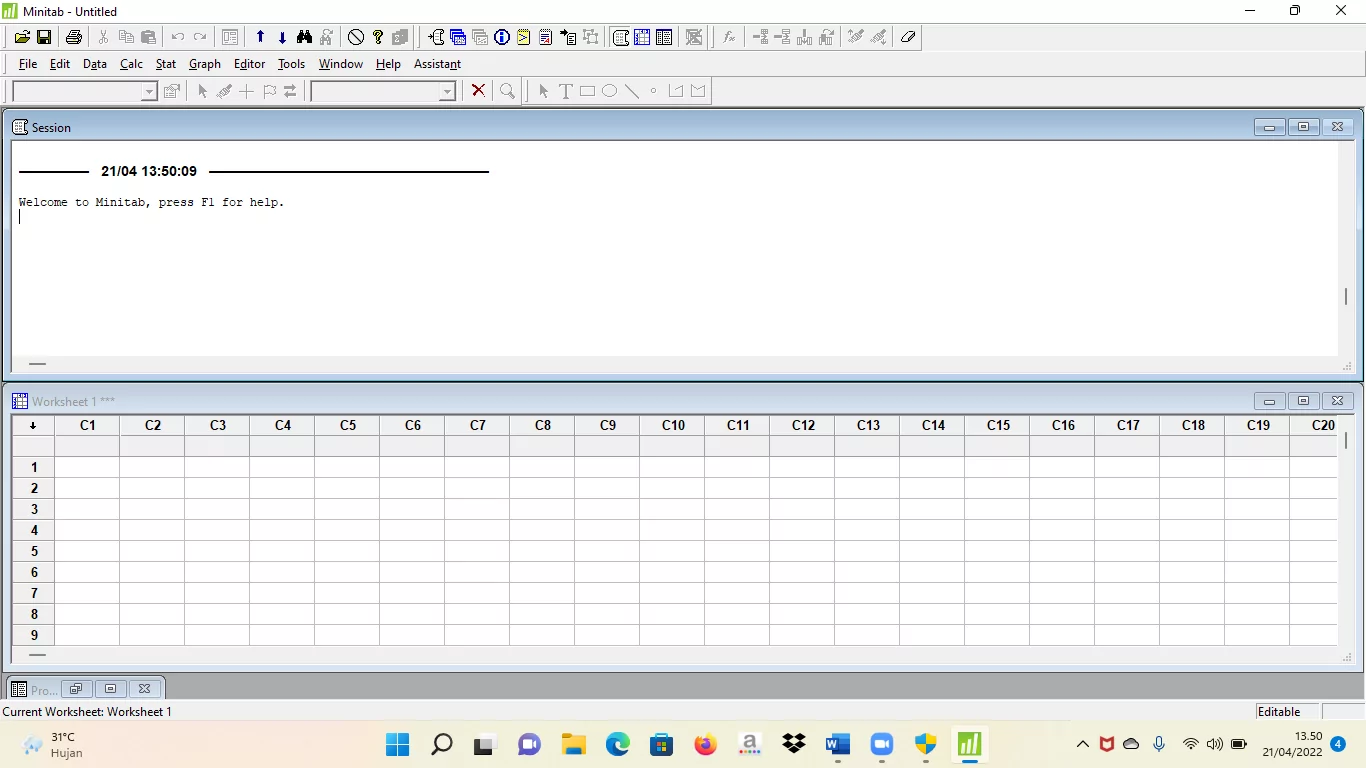
Minitab memiliki dua tampilan, yaitu worksheet dan session.
Worksheet adalah tempat untuk mengetikan data, sedangkan session adalah tempat untuk menampilkan semua perintah yang telah dialakukan dalam bentuk program dan hasil pengolahan data.
Hasil yang berupa grafik akan muncul berupa tab baru. Berikut tampilan dari software minitab.
Banyak kasus yang bisa diselesaikan menggunakan minitab ini, namun penulis hanya memberikan beberapa contoh cara menyelesaiakan kasus menggunakan minitab antaranya statitistik deskriptif, uji asumsi yang terdiri dari normalitas data dan uji homogenitas, dan uji hipotesis yang terdiri dari uji satu sampel (1-sampel-T) dan uji dua sampel (2-sampel-T)
1. STATISTIK DESKRIPTIF
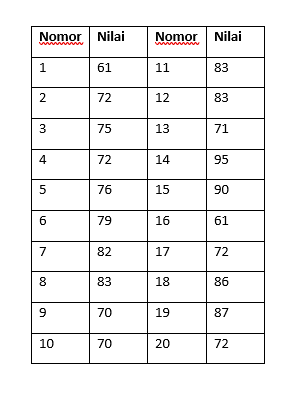
Berikut adalah data hasil UK-1 Mata Kuliah Pengantar Akuntansi dari mahasiswa Program Pendidikan Akuntansi.
Langkah-langkah untuk menampilka statistika deskriptif menggunakan minitab:
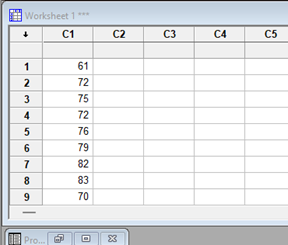
1. Ketikan semua data pada worksheet minitab
2. Pilih menu Stat – Basic Statistic – Display Descriptive Statistic
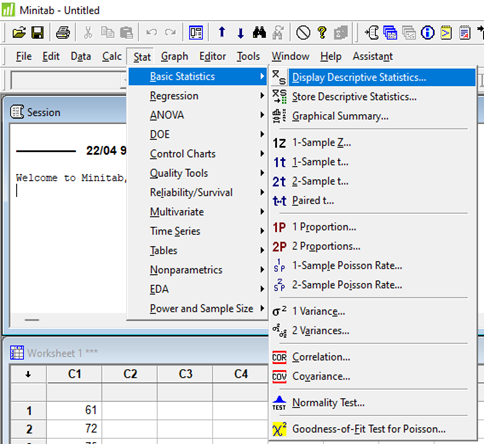
3. Masukan variable ‘Nilai’ ke dalam kotak variables, kemudian klik pilihan Statistic. Pilih statistic deskriptif apa saja yang akan diolah, kemudian ok
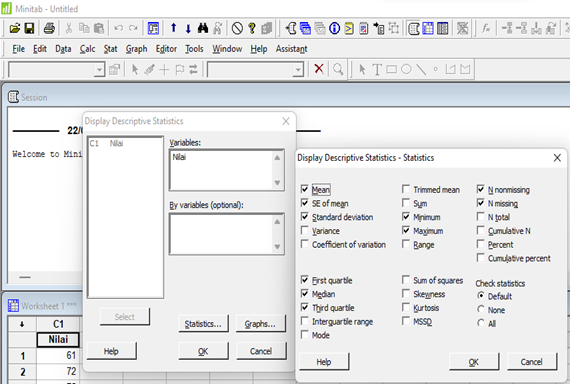
4. Jika ingin menampilkan grafik dari data tersebut, klik pilihan Graphs dan pilih grafik yang akan ditampilkan
5. Hasil yang keluar seperti di bawah ini
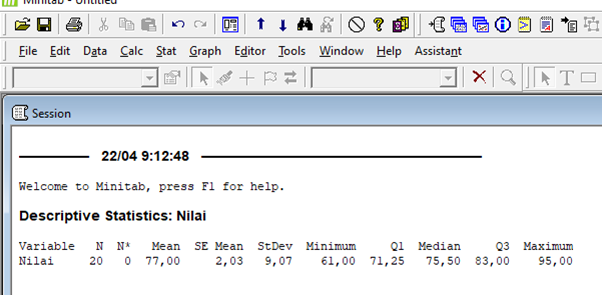
Dari hasil di atas diketahui bebrapa keterangan sebagai berikut:
a. Jumlah data nilai mata kuliah pengantar akuntansi yaitu 20
b. Mean atau rata-rata dari nilai mata kuliah pengantar akuntansi yaitu 77
c. Nilai terkecil yang diperoleh yaitu 61 dan nilai terbesar yang diperoleh yaitu 95
d. Median dari nilai mata kuliah pengantar akuntansi yaitu 75,5
e. Nilai Q1 yaitu 71,25 dan nilai Q3 yaitu 83
2. UJI ASUMSI
Normalitas Data
Saat kita akan melakukan uji hipotosis menggunakan statistic para metris, asusmsi yang harus dipenuhi adalah normalitas data.
Cara mengetahui bahwa data tersebut berdistribusi normal atau tidak bisa menggunakan minitab jika nanti hasil P- value nya > 0,05 maka data tersebut berdistribusi normal dan sebaliknya jika p-valuenya < 0,05 maka data tersebut tidak berdistribusi normal.
Dari data dibawah ini maka ujilah normalitasnya menggunakan minitab
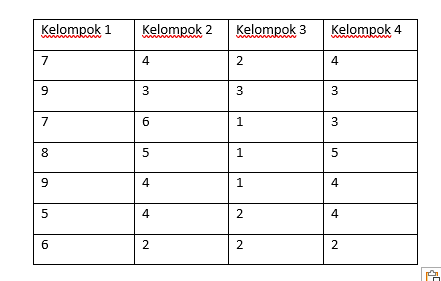
Langkah-langkah uji normalitas menggunakan minitab
1. Ketikan semua data nilai tersebut di kolom yang sudah diberi nama nilai dan dan disamping kolom nilai ketikan kelompok,
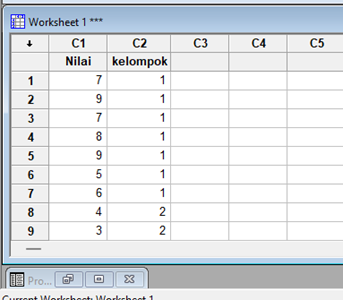
2. Ketik Stat – Basic Statistics – Normality Test
3. Masukan variable yang akan diuji normalitasnya, kemudian pilih jenis uji normalitas yang akan dilakukan, pada kolom title ketikan ‘uji normalitas’
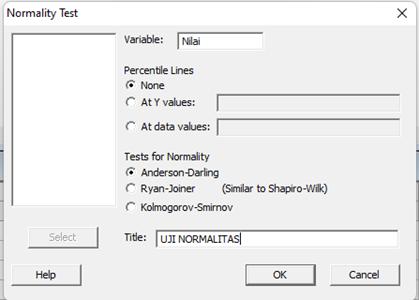
4. Hasil yang keluar sebagai berikut
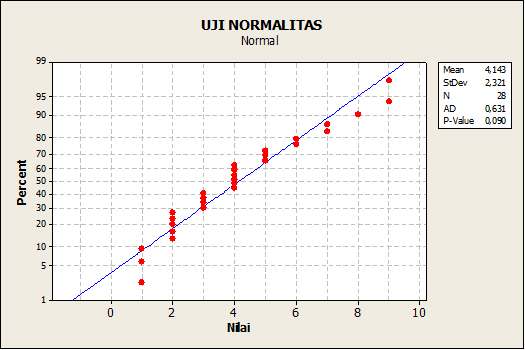
Hipotisis yang diuji adalah:
Ho : Data berdistribusi normal
Ha : Data tidak berdistribusi normal
Pada hasil di atas, diperoleh nilai p-value 0,00 yang berarti < 0,05 maka H0-Ditolak, kesimpulanya data tidak berdistribusi normal.
Menentukan normalitas juga bisa dilihat dari grafiknya, jika titik -titik menyebar mendekati sepanjang garis diagonal, maka bisa disimpulkan bahwa data berdistribusi normal dan sebaliknya.
Pada hasil di atas, terlihat beberapa titik di ujung atas dan bawah yang menjauh dari garis diagonal. Hal tersebut menunjukan data yang tidak berdistribusi normal.
Uji Homogenitas
Uji homogenitas ini digunakan untuk memperlihatkan bahwa dua atau lebih kelompo data sempel berasal dari populasi yang memiliki variansi yang sama.
Cara uji homogenitas dengan minitab yaitu:
1. Ketikan semua data nilai tersebut di kolom yang sudah diberi nama nilai dan dan disamping kolom nilai ketikan kelompok (saya manggunakan data pada contoh uji normalitas).
2. Katik Stat – Anova – Test For Equel Variances
3. Pada kolom response di klik nilai dan pada kolom factors di klik kelompok kemudian ok
4. Hasil yang keluar sebagai berikut
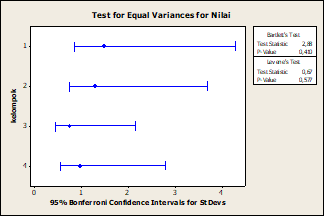
Hipotesis yang diuji :
Ho : Variansi pada tiap kelompok sama (homogen)
Ha: Varians pada tiap kelompok tidak sama (tidak homogen)
Lihat p-value Bonett’s Test, jika > 0,05 maka semua kelompok memiliki varians sama atau homogen berdasarkan rumus Bonett
Lihat p-value Levene’s Test, jika > 0,05 maka semua kelompok memiliki varians sama atau homogen berdasrkan rumus Levene
Dari hasil di atas nilai p-value dari uji Bonett 0,410, dan dari uji Levene 0,577. Kedua nilai tersebut lebih dari 0,05, jadi Ho di terima. Kesimpulanya keempat kelompok homogen.
3. UJI HIPOTESIS
Uji T Satu Sample (1-Sample T test)
Pengujian satu sample digunakan untuk menguji apakah rata-rata sebauh sampel berbeda secara signifikan atau tidak dengan nilai tertentu (yang diberikan sebagai pembanding).
Misalnya seorang peneliti akan menguji suatu hipotesis pada rata-rata nilai matkul Pengantar Akuntansi di universitas x adalah 75.
Untuk keperluan peneletian, peneliti mengambil nilai 20 mahasiswa di universitas x tersebut.
Untuk mengetahui hipotesis mana yang diterima , digunakan uji t.
Langkah-langkah uji satu sampel menggunakan minitab (penulis menggunakan sampel yang sama pada statistic deskriptif)
1. Ketikan semua data pada C4
2. Stat – Basic Statistics – 1-Sample t.
3. Pada Samples in colomns masukan sampel yang akan di uji, kemudian centang Perform hypothesis test masukan nilai rata-rata yang akan di uji, saat ini penulis akan menguji dengan 90
4. Klik pilihan Graphs, kemudian bisa pilih histogram atau boxplot untuk mengetahui sebaran datanya.
5. Klik ok
Hasil:
One-Sample T: C4
Test of mu = 90 vs not = 90
Variable N Mean StDev SE Mean 95% CI T P
C4 20 77,00 9,07 2,03 (72,76; 81,24) -6,4 0,000
Dari hasil uji nilai P-value 0,00 < 0,05, jadi Ho ditola.
Artinya , nilai rata-rata nilai UK 1 matkul Pengantar Akuntansi tidak sama satau berbeda secara signifikan dari nilai 90.
Garis di bawah X pada histogram menunjukan garis diterimanya nilai Ho. Dari grafik di atas terlihat bahwa nilai 90 berada di luar garis sehingga Ho ditolak.
Independen Sample T-Test (2-Sample-Test)
Two samplet T test digunakan untuk menguji signifikansi beda rata-rata dua kelompok yang saling bebas.
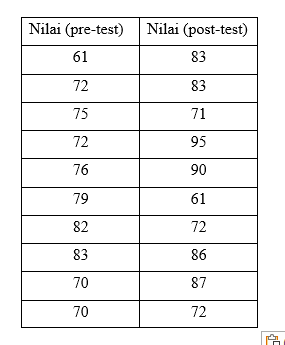
Misalnya Peneliti ingin mengetahui hasil dari penerapan sebuah model pembelajaran yang berbeda pada sebuah kelas, Peneliti memberikan pre-test dan post-test pada kelas tersebut. Berikut data nilai hasil pre-test dan post-test
Langkah pengujian dengan Minitab:
1. Masukan semua data pada kolom worksheet
2. Klik Stat – Basic Statiscs – 2sampel T.
3. Klik Samples in defferent columns kemudian pada kolom first di isi pre-test dan kolom second di isi post-test.
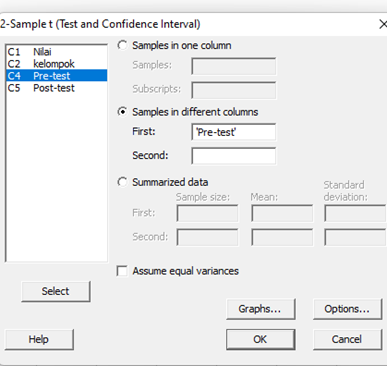
Hasil
Two-sample T for Pre-test vs Post-test
N Mean StDev SE Mean
Pre-test 10 74,00 6,53 2,1
Post-test 10 80,0 10,5 3,3
Difference = mu (Pre-test) – mu (Post-test)
Estimate for difference: -6,00
95% CI for difference: (-14,35; 2,35)
T-Test of difference = 0 (vs not =): T-Value = -1,53 P-Value = 0,147 DF = 15
Dari hasil di atas menunjukan bahwa rata-rata pre-test yaitu 74 dengan standar devisiasi 6,53 sedangkan rata-rata post-test yaitu 80 dengan standar devisiasi 10,5. P-value 0,147 > 0,05 maka Ho diterima.
Jadi, rata-rata nilai pre-test dan post-test tidak berbeda secara signifikan.